7、图（Graph）

图的表示、遍历以及最小生成树、最短路算法简介等

一、图

1.什么是图

表示“多对多”的关系，包含了：

• 一组顶点：通常用V(Vertex)表示顶点集合

• 一组边：通常用E(Edge)表示边的集合

• 无向边是顶点对：(v，w) ∈ E，其中v，w∈V

• 有向边<v,w>表示从v指向w的边(单行线)

• 不考虑重边和自回路

抽象数据类型定义

类型名称：图(Graph) 数据对象集：G(V,E)由一个非空的有限顶点集合V和一个有限边集合E组成。 操作集：对于任意图G ∈ Graph,以及 v ∈ V，e ∈ E

• Graph Create():建立并返回空图；

• Graph InsertVertex(Graph G, Vertex v)：将v顶点插入图G

• Graph InsertEdge(Graph G, Edge e):将边e插入图G

• void DFS(Graph G, Vertex v):从顶点v出发深度优先遍历图G；

• void BFS(Graph G, Vertex v):从顶点v出发广度优先遍历图G；

• void ShortestPath(Graph G, Vertex v, int Dist[]):计算图G中顶点v到其他任意顶点的最短距离；

• void MST(Graph G):计算图G的最小生成树 常用术语： 无向图、有向图、网络等……

怎样在程序中表示图

邻接矩阵

邻接矩阵的好处

• 直观、简单、好理解

• 方便检查任意一对顶点间是否存在边

• 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)

• 方便计算任一顶点的“度”(从该点发出的边数为“出度”，指向该点的边数为“入度”)

  • 无向图为对应行(或列)非0元素的个数

  • 有向图：对应行非0元素的个数是出度，对应列非0元素的个数是入度

邻接表

指针数组+链表，点很稀疏的时候很合算 邻接表的好处：

• 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)

• 节约稀疏图的空间

  • 需要N个头指针 + 2E个结点（每个结点至少2个域）

• 方便计算无向图任一顶点的“度”，但对有向图只能计算出度。

2.图的遍历

DFS深度优先搜索

深度优先搜索(Depth First Search,DFS),对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次. 伪代码描述：

void DFS(Vertex V) {
	visited[V] = true;
	for(v的每个邻接点W)
		if (!visited[W])
			DFS(W);
}

BFS广度优先搜索

广度优先搜索(Breadth First Search,BFS),借助队列(先进先出)来实现 伪代码描述：

void BFS(Vertex V) {
	visited[V] = true;
	Enqueue(V, Q);//将该顶点放入队列中
	while(!IsEmpty(Q)) {//当队列为空时结束搜索
		V = Dequeue(Q);//V为队首元素
		for(V的每个邻接点W) {
			if ( !visited[W] ) {
				visited[W] = true;//标记该点已访问
				Enqueue(W, Q);//将该点压入队列中
			}
		}
	}
}

图不连通怎么办？

• 路径：V到W的路径是一些列顶点{V，V1，V2，……，Vn，W}的集合，其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数(若带权，则是所有边的权重和)。若V到W之间的所有顶点都不同，则称为简单路径

• 连通：若V到W存在一条(无向)路径，则称V和W是连通的

• 回路：起点等于终点的路径

• 连通图：图中任意两顶点均连通

• 连通分量：无向图的极大连通子图

  • 极大顶点数：再加1个顶点就不连通了

  • 极大边数：包含子图中所有顶点相连的所有边

• 强连通：有向图中顶点V和W之间存在双向路径，则称V和W是强连通的

• 强连通图：有向图中任意两顶点均强连通

• 强连通分量：有向图的极大强连通子图

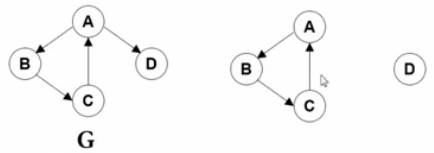
每调用一次DFS，其实就是把V所在的连通分量遍历了一遍。BFS也一样。

void ListComponents ( Graph G ) {//遍历连通分量
	for (each V in G)
		if ( !visited[V] ) {
			DFS( V );
		}
}

3.如何建立图

(1) 邻接矩阵表示的图的建立

定义

const int MaxVertexNum = 100;
typedef int DataType;
typedef bool WeightType;
typedef struct GNode *PtrToGNode;
struct GNode {
    int Nv;//顶点数
    int Ne;//边数
    WeightType G[MaxVertexNum][MaxVertexNum];
    DataType Data[MaxVertexNum];//存顶点的数据
};
typedef PtrToGNode MGraph;//以邻接矩阵存储的图类型

初始化

初始化一个有VertexNum个顶点但没有边的图

typedef int Vertex;
MGraph CreateGraph(int VertexNum) {
    Vertex V, W;
    MGraph Graph;
    Graph = (MGraph) malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    //顶点编号从0开始，到Graph->Nv-1
    for (V = 0; V < Graph->Nv; V++) {
        for(W = 0; W < Graph->Nv; W++) {
            Graph->G[V][W] = 0; //有向图中可改0为INF等
        }
    }
    return Graph;
} 

向图中插入边

边的定义

typedef struct ENode *PtrToENode;
struct ENode {
    Vertex V1, V2;//有向边<V1,V2>
    WeightType Weight;//权重
};
typedef PtrToENode Edge;

插入操作

void InsertEdge(MGraph Graph, Edge E) {
    //插入边<V1,V2>
    Graph->G[E->V1][E->V2] = E->Weight;
    //若为无向图，则还要插入边<V2,V1>
    Graph->G[E->V2][E->V1] = E->Weight;
}

完整的建立一个MGraph

输入格式

Nv Ne V1 V2 Weight ……

MGraph BuildGraph() {
    MGraph Graph;
    Edge E;
    Vertex V;
    int Nv;
    cin >> Nv;
    Graph = CreateGraph(Nv);//建立有Nv个顶点的图
    cin >> Graph->Ne;//边数Ne
    if(Graph->Ne != 0) {
        E = (Edge)malloc(sizeof(struct ENode));
        for (int i = 0; i < Graph->Ne; i++) {
            cin >> E->V1 >> E->V2 >> E->Weight;
            InsertEdge(Graph, E);
        }
    }
    //如果顶点有数据的话，读入数据
    for(V = 0; V < Graph->Nv; V++) {
        cin >> Graph->Data[V];
    }
    return Graph;
}

(2) 邻接表表示的图的建立

可在邻接矩阵的基础上进行修改

定义

const int MaxVertexNum = 100;
typedef int DataType;
typedef int Vertex;
typedef bool WeightType;
//邻接表定义
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode {
    Vertex AdjV;//邻接点下标
    WeightType Weight;//边权重
    PtrToAdjVNode Next;
};

typedef struct VNode {
    PtrToAdjVNode FirstEdge;
    DataType Data;//存顶点的数据
}AdjList;

typedef struct GNode *PtrToGNode;
struct GNode {
    int Nv;//顶点数
    int Ne;//边数
    AdjList G;//邻接表
};
typedef PtrToGNode LGraph;//以邻接表存储的图类型

LGraph初始化

LGraph CreateGraph(int VertexNum) {
    Vertex V, W;
    LGraph Graph;
    Graph = (LGraph) malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    //顶点编号从0开始，到Graph->Nv-1
    for (V = 0; V < Graph->Nv; V++) {
        Graph->G[V].FirstEdge = NULL;
    return Graph;
}

向LGraph中插入边

typedef struct ENode *PtrToENode;
struct ENode {
    Vertex V1, V2;//有向边<V1,V2>
    WeightType Weight;//权重
};
typedef PtrToENode Edge;
void InsertEdge(LGraph Graph, Edge E){
    PtrToAdjVNode NewNode;
    //插入边<V1,V2>
    //为V2建立新的邻接点
    NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    //将V2邻接点插入V1的表头
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
    
    //若为无向图 则还要插入边<V2,V1>
    //为V2建立新的邻接点
    NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    //将V2邻接点插入V1的表头
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
}

完整的建立一个LGraph

仅需将MGraph换成LGraph，将存Data是稍作更改即可

LGraph BuildGraph() {
    LGraph Graph;
    Edge E;
    Vertex V;
    int Nv;
    cin >> Nv;
    Graph = CreateGraph(Nv);//建立有Nv个顶点的图
    cin >> Graph->Ne;//边数Ne
    if(Graph->Ne != 0) {
        E = (Edge)malloc(sizeof(struct ENode));
        for (int i = 0; i < Graph->Ne; i++) {
            cin >> E->V1 >> E->V2 >> E->Weight;
            InsertEdge(Graph, E);
        }
    }
    //如果顶点有数据的话，读入数据
    for(V = 0; V < Graph->Nv; V++) {
        cin >> Graph->G[V].Data;
    }
    return Graph;
}

二、最短路径问题

1.概念简介

• 在网络中，求两个不同顶点之间的所有路径中，边的权值之和最小的那一条路径

  • 这条路径就是两点之间的最短路径(Shortest Path)

  • 第一个顶点叫源点(Source)

  • 最后一个顶点叫终点(Destination)

2.问题分类

• 单源最短路径问题：从某固定源点出发，求其到所有其他顶点的最短路径

  • (有向)无权图

  • (有向)有权图

• 多源最短路径问题：求任意两顶点之间的最短路径

2.无权图的单源最短路算法

按照递增的顺序找出到各个顶点的最短路，与BFS思想很类似！ 首先需要定义一个数组dist,dist[W]存储S到W的最短距离，S为起点，dist[S]=0，dist需要被初始化成一个-1(或无穷)，便于后来的判别是否被访问过。 其次需要定义数组path,path[W]存储S到W的路上经过的某顶点。 dist和path数组都需先被初始化为-1~然后将起点的dist[S]设为0，压入队列开始访问 伪代码：

void Unweighted(Vertex S) {
	Enqueue(S, Q);
	while(!IsEmpty(Q)) {
		V = Dequeue(Q);
		for (V的每个邻接点W)
			if(dist[W] == -1) {
				dist[W] = dist[V]+1;
				path[W] = V;
				Enqueue(W, Q);
			}
	}
}

3.有权图的单源最短路算法

在这里插入图片描述

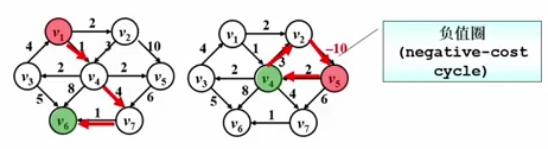
Dijkstra算法！

• 令s={源点s + 已经确定了最短路径的顶点vi }

• 对任一未收录的顶点v定义dist[v]为s到v的最短路径长度，但该路径仅经过S中的顶点，即路径{s→(vi∈S)→v}的最小长度

• 若路径是按照递增的顺序生成的，则

  • 真正的最短路必须只经过S中的顶点(反证法可证)

  • 每次从未收录的顶点中选一个dist最小的收录(贪心)

  • 增加一个v进入S,可能会影响另外一个w的dist值！(所以要检查v的所有邻接点w！)

    • dist[w] = min{ dist[w]，dist[v] + <v,w>的权重} dist初始化：S的所有邻接点W的dist都可初始化为s与w的权重，其他则定义为正无穷。

伪代码描述：

void Dijkstra(Vertex s) {
	while (1){
		V = 未收录顶点中dist最小者;
		if (这样的V不存在)
			break;
		collected[V] = true;
		for (V的每个邻接点W)
			if(collected[W] == false)
				if(dist[V] + E<v,w> < dist[W]) {
					dist[W] = dist[V]+E<v,w>;
					path[W] = V;
				}
	}
}//不能解决有负边的情况

伪代码中dist[W]=dist[V]+E~<V,W>~；并不是简单的赋值，而是如果有了更短的距离，需要将其更新成为更短的距离

Dijkstra核心代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
const int inf  = 0x3f3f3f;
int T,N,x,y,z;
int edge[maxn][maxn];
int dist[maxn];
bool vis[maxn];
void init() {
    for(int i = 1; i <= N; ++i) {
        for(int j = 1; j <= N; ++j) {
            edge[i][j] = inf;
        }
        edge[i][i] = 0;
    }
}
void Dijstra(int u) {
    for(int i = 1; i <= N; ++i) {
        vis[i] = false;
        dist[i] = edge[u][i];
    }
    vis[u] = true;
    for(int i = 1; i <= N; ++i) {
        int t, mindis = inf;
        for(int j = 1; j <= N; ++j) {
            if(!vis[j] && dist[j] < mindis) {
                mindis = dist[j];
                t = j;
            }
        }
        vis[t] = true;
        for(int j = 1; j <= N; ++j) 
            if(!vis[j] && dist[j] > edge[t][j] + dist[t]) 
                dist[j] = edge[t][j] + dist[t];
    }
}

三、最小生成树

1.什么是最小生成树(Minimum Spanning Tree)

• 是一棵树

  • 无回路

  • |V|个顶点一定有|V|-1条边

• 是生成树

  • 包含全部顶点

  • |V|-1条边都在图里

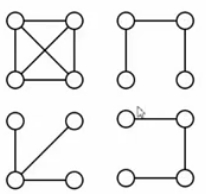
  • 向生成树中任加一条边都一定构成回路

• 边的权重和最小

最小生成树与图连通等价

2.解决最小生成树问题

通常离不开贪心算法：

• “贪”：每一步都要最好的

• “好”：权重最小的边

• 需要约束：

  • 只能用图里有的边

  • 只能正好用掉|V|-1条边

  • 不能有回路

放到了另一篇博客里。 图论——解决最小生成树问题(Kruskal算法&Prim算法)