day6：33. 搜索旋转排序数组、54. 螺旋矩阵、bytedance-006. 夏季特惠

day6题目：33. 搜索旋转排序数组、54. 螺旋矩阵、bytedance-006. 夏季特惠

学习计划链接：冲刺春招-精选笔面试 66 题大通关

今日知识点：二分、模拟、01背包，难度为中等、中等、字节の简单

33. 搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1： 输入：nums = [4,5,6,7,0,1,2], target = 0 输出：4

示例 2： 输入：nums = [4,5,6,7,0,1,2], target = 3 输出：-1

示例 3： 输入：nums = [1], target = 0 输出：-1

思路

两次二分，第一次查找分界点如例1、2中的0（153. 寻找旋转排序数组中的最小值），分界点左侧数一定都比右侧大且为升序，故根据target与第一个数比较判断在左侧找还是右侧找。注意特判一下nums[n-1] > nums[0]的情况（即旋转多次回到原数组的情况）

代码

class Solution {
public:
    int binarySearch(vector<int>& nums, int target, int s, int e) {
        int l = s, r = e;
        while(l <= r) { 
            int mid = (l+r)>>1;
            if(nums[mid] == target) return mid;
            if(nums[mid] < target) l = mid+1;
            else r = mid-1;
        }
        return -1;
    }
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        int l = 0, r = n-1;
        int idx;
        if(nums[r] > nums[l]) idx = n-1;
        else {
            while(l < r) { // 找分界点 如0
                int mid = (l+r)>>1;
                if(nums[mid] == target) return mid;
                if(nums[mid] > nums[l]) l = mid;
                else r = mid;
            }
            idx = l;
        }
        if(target < nums[0])
            return binarySearch(nums, target, idx+1, n-1);
        else 
            return binarySearch(nums, target, 0, idx);
    }
};

54. 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

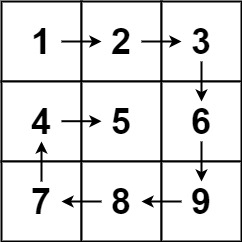
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,2,3,6,9,8,7,4,5]

思路

某蓝桥杯经典真题稍稍变形- - 模拟每次就一直往右下左上的顺序走就行了

代码

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function(matrix) {
    let m = matrix.length;
    let n = matrix[0].length;
    let sum = n*m;
    let vis = -200;
    let ans = [matrix[0][0]];
    matrix[0][0] = vis;
    let [i, j] = [0, 0];
    let cnt = 1;
    while(cnt < sum) {
        while(j+1 < n && matrix[i][j+1] != vis) {   // 往右走
            ans.push(matrix[i][j+1]);
            matrix[i][++j] = vis;
            ++cnt;
        }
        while(i+1 < m && matrix[i+1][j] != vis) {  // 往下走
            ans.push(matrix[i+1][j]);
            matrix[++i][j] = vis;
            ++cnt;
        }
        while(j-1 >= 0 && matrix[i][j-1] != vis) {  // 往左走
            ans.push(matrix[i][j-1]);
            matrix[i][--j] = vis;
            ++cnt;
        }
        while(i-1 >= 0 && matrix[i-1][j] != vis) {  // 往上走
            ans.push(matrix[i-1][j]);
            matrix[--i][j] = vis;
            ++cnt;
        }
    }
    return ans;
};

bytedance-006. 夏季特惠

某公司游戏平台的夏季特惠开始了，你决定入手一些游戏。现在你一共有X元的预算，该平台上所有的 n 个游戏均有折扣，标号为 i 的游戏的原价a[i]元，现价只要 b[i] 元（也就是说该游戏可以优惠 a[i]-b[i] 元）并且你购买该游戏能获得快乐值为 w[i] ，由于优惠的存在，你可能做出一些冲动消费导致最终买游戏的总费用超过预算，但只要满足获得的总优惠金额不低于超过预算的总金额，那在心理上就不会觉得吃亏。现在你希望在心理上不觉得吃亏的前提下，获得尽可能多的快乐值。

• 输入

  • 第一行包含两个数 n 和 x 。

  • 接下来 n 行包含每个游戏的信息，原价 ai , 现价 bi，能获得的快乐值为 wi 。

• 输出

  • 输出一个数字，表示你能获得的最大快乐值。

示例 1： 输入： 4 100 100 73 60 100 89 35 30 21 30 10 8 10 输出：100 解释：买 1、3、4 三款游戏，获得总优惠 38 元，总金额 102 元超预算 2 元，满足条件，获得 100 快乐值。

示例 2： 输入： 3 100 100 100 60 80 80 35 21 21 30 输出：60 解释：只能买下第一个游戏，获得 60 的快乐值。

思路

经典01背包问题，难点在于如何转换成背包问题qwq，看了题解才晓得 背包问题可看这篇博客：01背包问题详解（浅显易懂） 由题意易知（其实想了半天）每买一个游戏都会使预算加上该游戏的优惠价，再从预算里减掉现价，那么设优惠价为dis，若当前游戏优惠价 >= 现价的话买了是绝对不亏的（预算反而增加了），否则就将该游戏视作等待进行01背包的一员（取或不取） 还要注意下数据范围，w贼大，所以要用long long

完整代码

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 505;
const int maxm = 3e5;
int n, x, a, b, c, cnt;  // x为预算
int v[maxn];// 容量
ll ans, w[maxn];
int main() {
    cin >> n >> x;
    for(int i = 0; i < n; ++i) {
        cin >> a >> b >> c;    // 原价 现价 快乐值
        int dis = a-b;    // 优惠 每买一个游戏都会使预算加上优惠价，再从预算里减掉现价。
        if(dis > b) { // 所以优惠价大于现价的话一定买
            x += dis-b;
            ans += c;
        } else {
            v[cnt] = b-dis;
            w[cnt++] = c;
        }
    }
    vector<ll> dp(maxm, 0);
    for(int i = 0; i < cnt; ++i) {
        for(int j = x; j >= v[i]; --j) {
            dp[j] = max(dp[j], dp[j-v[i]]+w[i]);
        }
    }
    ans += dp[x]; 
    cout << ans << endl;
    return 0;
}