9、散列表（hash）

1.概念引出

编译处理中对变量的管理：动态查找问题

• 利用查找树进行？——两个变量名（字符串）比较效率不高

• 将字符串转换为数字，再处理？——即为散列查找的思想 已知的几种查找方法：

• 顺序查找 O(N)

• 二分查找（静态查找） O(log2N)

• 二叉搜索树 O(h) h为二叉查找树的高度

• 平衡二叉树 O(log2N)

在这里插入图片描述

问题：如何快速搜索到需要的关键词？若关键词不方便比较怎么办？

查找的本质： 已知对象找位置

• 有序的安排对象：全序（完全有序，eg:二分搜索）、半序（某些关键词之间存在次序，eg:查找树）

• 直接 “算出” 对象位置：散列

散列基本工作

• 计算位置：构造散列函数确定关键词存储位置

• 解决冲突：应用某种策略解决多个关键词位置相同的问题

时间 复杂度

时间复杂度几乎是常量：O(1)，即查找时间与问题规模无关！

2.散列查找

（1）基本思想

• 以关键字key为自变量，通过一个确定的函数h （散列函数），计算出对应的函数值h(key)，作为数据对象的存储地址

• 可能不同的关键字会映射到同一个散列地址上，即h(keyi) = h(keyj) (当keyi ≠ keyj)，称为 “冲突(Collision)” 。——需要某种冲突解决策略

不冲突的情况下，查找只需要根据散列函数算出地址查找

装填因子

装填因子（Loading Factor）：设散列表空间大小为m，填入表中元素个数为n，则称 α = n / m为散列表的装填因子

• 如上图中的α = 11 / 17 ≈ 0.65 如果没有溢出 则T查询 = T插入 = T删除 = O(1)

再散列

• 当散列表元素过多（即装填因子α过大）时，查找效率会下降

  • 实用最大装填因子一般取0.5 ≤ α ≤ 0.85

• 解决办法是加倍扩大散列表，该过程叫做“再散列(Rehashing)”

（2）散列函数的构造

两个因素

一个“好”的散列函数一般应考虑以下两个因素：

• 计算简单，以便提高转换速度

• 关键词对应的地址空间分布均匀，以尽量减少冲突。

数字关键词的散列函数构造

① 直接定址法

取关键词的某个线性函数值为散列地址，即h(key) = a ×key + b (a、b为常数)

② 除留余数法（常用）

散列函数为：h(key) = key mod p eg：h(key) = key %17 一般为了尽可能使关键词对应的地址空间分布均匀，p取素数

③ 数字分析法

通过分析数字关键字在各位上的变化情况，取比较随机的位作为散列地址

在这里插入图片描述

④ 折叠法

把关键词分割成位数相同的几个部分，然后叠加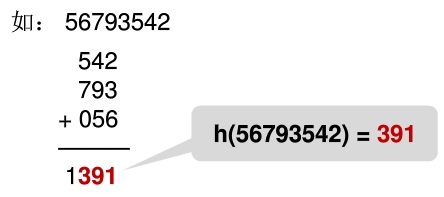

⑤ 平方取中法

把关键词分割成位数相同的几个部分，然后叠加

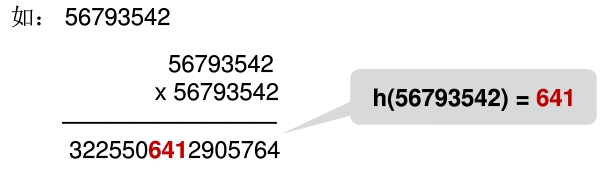
字符关键词的散列函数构造

简单的散列函数——ASCII码加合法

对字符型关键词key定义散列函数如下：h(key) = (Σkey[i]) mod TableSize 冲突严重！！

简单的改进——前3个字符移位法

h(key) = (key[0] × 27^2^ + key[1] ×27 + key[2]) mod TableSize 仍然冲突、空间浪费

好的散列函数——移位法

设计关键词的所有n个字符，且分布的很好 h(key) = ($\begin{matrix} \sum_{i=0}^{n-1}key[n-i-1] \times32^i \end{matrix}$) mod TableSize 代码如下

typedef string DataType;//数据的类型
typedef int Index;//散列后的下标
//返回经散列函数计算后的下标
Index Hash(string Key, int TableSize) { 
    unsigned int h = 0; //散列函数值，初始化为0
    int len = Key.length();
    for(int i = 0; i < len; ++i) 
        h = (h << 5) + Key[i];
    
    return h % TableSize;
}

（3）散列查找的冲突处理

常用处理冲突的思路如下

• 换个位置——开放定址法

• 同一位置的冲突对象组织在一起——链地址法

开放定址法

开放定址法(Open Addressing)，一旦产生了冲突（该位置已有其他元素），则按某种规则去寻找另一空地址。其优点是散列表是一个数组，存储效率高，随机查找，缺点是散列表有“聚集”现象。在开放地址散列法中删除操作需要很小心，只能“懒惰删除”，即需要增加一个删除标记而不是真正的删除，以便查找时不会“断链”。其空间可以在下次插入时重用。

• 若发生了第 i 次冲突，试探的下一个地址将增加di，基本公式是：hi(key) = (h(key) + di) mode TableSize(1 ≤ i < TableSize)

• di 为多少决定了不同的解决冲突方案：线性探测(di = i)、平方探测(di = ± i^2^)、双散列(di = i*h2(key))。

① 线性探测法

以增量序列1，2，……，（TableSize - 1）循环试探下一个存储地址。

在这里插入图片描述

在这里插入图片描述

② 平方探测法（二次探测）

以增量序列1^2^，-1^2^，2^2^，-2^2^，……，q^2^，-q^2^且q ≤ | TableSize/2 |循环试探下一个存储地址。 平方探测是否能找得到所有空间？有定理如下：

• 如果散列表长度TableSize是某个4k+3（k是正整数）形式的素数时，平方探测法就可以探查到整个散列表空间

//查找Key元素,这里采用平方探测法处理冲突
Index Find(ptrHash H, DataType Key) {
    Index nowp, newp;
    int Cnum = 0;//记录冲突次数
    newp = nowp = Hash(Key, H->TableSize);
    //若该位置的单元非空且不是要找的元素时发生冲突
    while(H->Units[newp].flag != Empty && H->Units[newp].data != Key) {
        ++Cnum;//冲突增加一次
        if(++Cnum % 2) {
            newp = nowp + (Cnum+1)*(Cnum+1)/4;//增量为+i^2,i为(Cnum+1)/2
            if(newp >= H->TableSize)
                newp = newp % H->TableSize;
        } else {
            newp = nowp - Cnum*Cnum/4;//增量为-i^2,i为Cnum/2
            while(newp < 0)
                newp += H->TableSize;
        }
    }
    return newp;//返回位置，该位置若为一个空单元的位置则表示找不到
}

③ 双散列探测法

di为i*h2(key)，h2(key)是另一个散列函数，探测序列成h2(key)，2h2(key)，3h2(key)……

• 对任意的key，h2(key) ≠ 0！

• 探测序列还应该保证所有的散列存储单元都应该能够被探测到，选择以下形式有良好的效果：h2(key) = p - (key mod p) 其中p < TableSize，p、TableSize都是素数

分离链接法

分离链接法(Separate Chaining)，将相应位置上冲突的所有关键词存储在一个单链表中。优点是关键字的删除不需要“懒惰删除法”从而没有存储垃圾，缺点是链表部分的存储效率和查找效率都比较低。链表长度的不均匀会导致时间效率的严重下降

（4）散列查找的操作集（代码）

这里给出字符串的散列查找，Hash函数采用移位法，解决冲突采用开放定址法中的平方探测法，其他的在其基础上更改即可

定义

const int MaxSize = 100000;
typedef int Index;//散列后的下标
typedef string DataType;//散列单元中存放的元素类型
//散列单元状态类型，分别对应：有合法元素、空单元、有已删除元素
typedef enum {Legitimate, Empty, Deleted} EntryType;
struct HashNode {   //散列表单元类型
    DataType data;      //存放元素
    EntryType flag;     //单元状态
};
struct HashTable {  //散列表类型
    int TableSize;      //表长
    HashNode *Units;	//存放散列单元的数组
};
typedef HashTable *ptrHash;

获取素数

返回大于N且不超过MaxSize的最小素数，用于保证散列表的最大长度为素数，尽可能使关键词对应的地址空间分布均匀

//返回大于N且不超过MaxSize的最小素数，用于保证散列表的最大长度为素数
int NextPrime(int N) {
    int i, p = (N%2) ? N+2 : N+1;//从大于N的下一个奇数p开始
    while(p <= MaxSize) {
        for(i = (int)sqrt(p); i >= 2; i--) 
            if(!(p % i)) break;//不是素数
        if(i == 2) break;//for正常结束，是素数
        else p += 2;//试探下一个奇数
    }
    return p;
}

创建空表

创建一个长度大于TableSize的空表。（确保长度为素数）

ptrHash CreateTable(int TableSize) {
    ptrHash H;
    int i;
    H = new HashTable;
    H->TableSize = NextPrime(TableSize);
    H->Units = new HashNode[H->TableSize];
    for(int i = 0; i < H->TableSize; ++i) 
        H->Units[i].flag = Empty;
    return H;
}

Hash计算

返回经散列函数计算后的下标 这里关键字数据类型为string,采用移位法散列

Index Hash(DataType Key, int TableSize) { 
    unsigned int h = 0; //散列函数值，初始化为0
    string str = Key.str;
    int len = str.length();
    for(int i = 0; i < len; ++i) 
        h = (h << 5) + str[i];
    return h % TableSize;
}

查找操作

查找Key元素,这里采用平方探测法处理冲突，返回位置下标，该位置若为一个空单元的位置则表示找不到

Index Find(ptrHash H, DataType Key) {
    Index nowp, newp;
    int Cnum = 0;//记录冲突次数
    newp = nowp = Hash(Key, H->TableSize);
    //若该位置的单元非空且不是要找的元素时发生冲突
    while(H->Units[newp].flag != Empty && H->Units[newp].data != Key) {
        ++Cnum;//冲突增加一次
        if(++Cnum % 2) {
            newp = nowp + (Cnum+1)*(Cnum+1)/4;//增量为+i^2,i为(Cnum+1)/2
            if(newp >= H->TableSize)
                newp = newp % H->TableSize;
        } else {
            newp = nowp - Cnum*Cnum/4;//增量为-i^2,i为Cnum/2
            while(newp < 0)
                newp += H->TableSize;
        }
    }
    return newp;//返回位置，该位置若为一个空单元的位置则表示找不到
}

插入操作

将Key插入到表中，返回插入成功或失败，失败则说明该键值已存在

bool Insert(ptrHash H, DataType Key) {
    Index p = Find(H, Key);
    if(H->Units[p].flag != Legitimate) {//该位置可插入元素
        H->Units[p].flag = Legitimate;
        H->Units[p].data = Key;
        //其他操作
        return true;
    } else {//该键值已存在
        //其他操作
        return false;
    }
}

（5）性能分析

散列表的查找效率通过以下因素分析：

• 成功平均查找长度（ASLs）

• 不成功平均查找长度（ASLu）

以线性探测法中的例题为例分析如下这个散列表的性能

在这里插入图片描述

• 其ASLs为查找表中关键词的平均查找比较次数（即其冲突次数加1） ASLs = （1+7+1+1+2+1+4+2+4）/ 9 = 23 / 9 ≈ 2.56

• 其ASLu为不在散列表中的关键词的平均查找比较次数（不成功） 一般方法：将不在散列表中的关键词分若干类，如按其H(key)值分类的话，此处的H(key) = key mod 11，分11类分析，ASLu如下 ASLu = （3+2+1+2+1+1+1+9+8+7+6）/ 11 = 41 / 11 ≈ 3.73

关键词的比较次数，取决于产生冲突的多少，而影响产生冲突多少有以下三个因素

1. 散列函数是否均匀

2. 处理冲突的方法

3. 散列表的装填因子α 不同冲突处理方法和装填因子对于效率的影响如下

① 线性探测法的查找性能

在这里插入图片描述

② 平方探测法和双散列探测法的查找性能

当装填因子α<0.5时，各种探测法的期望探测次数都不大，也比较接近，随着α的增大，线性探测法的期望探测次数增加较快，不成功查找和插入操作的期望探测次数要比成功查找的期望探测次数要大。所以，合理的最大装入因子应该不超过0.85

③ 分离链接法的查找性能

在这里插入图片描述

总结

• 选择合适的h(key)的话，散列法的查找效率期望是常数O(1)，它几乎与关键字的空间的大小n无关！也适合于关键字直接比较计算量大的问题

• 它是以较小的α为前提，因此，散列方法是一个以空间换时间的方法

• 散列方法的存储对关键字是随机的，不便于顺序查找关键字，也不适合于范围查找，或最大值最小值查找。