day4题目：1. 两数之和、15. 三数之和、42. 接雨水
今日知识点：数组、双指针、单调栈，难度仍为简单、中等、困难
学习计划链接：冲刺春招-精选笔面试 66 题大通关
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1： 输入：nums = [2,7,11,15], target = 9 输出：[0,1] 解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
思路
做烂了都,hash存一下出现过的下标，出现过则返回这一对
完整代码
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
let m = new Map();
let len = nums.length;
for(let i = 0; i < len; ++i) {
let nowp = nums[i];
if(m.has(target-nowp)) {
return [m.get(target-nowp), i];
} else m.set(nowp, i);
}
};
15. 三数之和
给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。
示例 1： 输入：nums = [-1,0,1,2,-1,-4] 输出：[[-1,-1,2],[-1,0,1]]
思路
有个小坑，js例排序不指定排序规则函数的话默认是以字符串形式从小到大排序的~ 遍历+双指针防止重复，重复的就跳过。
完整代码
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
nums.sort((a, b) => a-b);
let len = nums.length;
let ans = []
for(let i = 0; i < len; ++i) {
if(i > 0 && nums[i] === nums[i-1]) continue; // 不重复枚举
let tar = -nums[i];
let r = len-1;
for(let l = i+1; l < len; ++l) {
if(l > i+1 && nums[l] === nums[l-1]) continue; // 不重复枚举
while(l < r && nums[l]+nums[r] > tar) --r;
if(l === r) break;
if(nums[l]+nums[r] === tar) {
ans.push([nums[i], nums[l], nums[r]]);
}
}
}
return ans;
};
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1： 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出：6 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
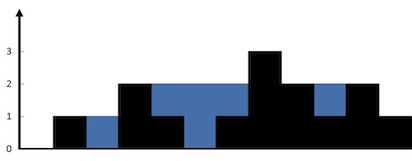
思路
单调栈，维护一个单调递减的栈(存的是下标)，遍历高度数组 h[r]，每次与栈顶比较，若栈不为空且 h[r] 大于栈顶，则将栈顶出栈为 top ，若此时栈为空则说明前面没有能挡住水的地方故不需计算结束，将 h[r] 入栈；若不为空则将此时的栈顶元素即 l 与当前元素 r 比较高度，取较矮的那个（min(height[l], height[r])）减去 h[top] 作为高度，宽度则为 r-l-1，
完整代码
/**
* @param {number[]} height
* @return {number}
*/
var trap = function(height) {
let s = []; // 存下标
let ans = 0;
let l = 0;
let n = height.length;
for(let r = 0; r < n; ++r) {
let size = s.length;
while(size != 0 && height[r] > height[s[size-1]]) { // 跟栈顶比较
let top = s.pop(); // 栈顶出
--size;
if(size == 0) break;
l = s[size-1]; // 为栈顶底下的一个元素
ans += (r-l-1)*(Math.min(height[l], height[r]) - height[top]); // 宽*高
}
s.push(r); // 小于等于栈顶，则进栈
}
return ans;
};
